Immersed Boundary Method
The Immersed Boundary (IB) Method is a method to solve CFD equations for a body immersed in a fluid (thus the name). This method extremely useful for solving problems involving bluff bodies. Sharp or aerodynamic bodies can also be solved through some modifications. This method was initially introduced by Professor Peskin at the Courant Institute of Mathematics at NYU. The original problem was to simulated the flow inside a heart. The link to Professor Peskin’s work is here.
The greatest advantage of the above method is it allows us to solve the CFD equations on a regular cartesian grid as opposed to a body fitted grid which would be need for a method like SIMPLE.
The method relies on the introducing an artificial forcing function to the momentum equation when there is a boundary present. The presence of a boundary is told to the equation using a Dirac function.
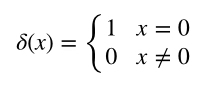 |
The above is the Dirac function in 1D. This can obviously be extended to 2D and 3D by multiplying the Dirac function for each dimension. Example:
\[ \delta_{2D}(x,y) = \delta(x) \delta(y)\]
\[ \delta_{3D}(x,y) = \delta(x) \delta(y) \delta(z)\]
The recast incompressible fluid equations would be the following:
Continuity : $latex \Delta \cdot \textbf{u} = 0$
Momentum: $latex \dfrac{\partial \textbf{u}}{\partial t} + \textbf{u} \cdot \dfrac{\partial \textbf{u}}{\partial \textbf{x}} = \dfrac{1}{\rho}\Delta p + \nu \Delta^2 \textbf{u} + \textbf{g} + \displaystyle \int_{d\Omega} \textbf{u}_b(s) \delta_{3D}(\textbf{x} - \xi (s)) ds $
which are valid is the domain space $latex \mathbb{R}^3$
In the above equation, all terms and symbols have their usual meaning. $latex \textbf{u}_b$ describes the velocity of the fluid on the object. Of course, from basic fluid dynamics, we know that we cannot allow the fluid to slip over or penetrate the body. So the $latex \textbf{u}_b$ must be the velocity of the body. In more technical terms, this process is called mapping. We are mapping the velocity of the body to the velocity field of the domain.
$latex \xi(s)$ is a function for the geometry of the body. From what we learnt about the Dirac function above, $latex \textbf{x} = \xi(s)$ for $latex \delta_{3D} = 1$. Otherwise, the momentum equation reduces to the standard form. Thus, this additional force only acts when we are evaluating at the boundary of the object.
Further, we have to ensure that the vice-versa is also true, i.e., the velocity field mapped on to the body yields the velocity of the body. Mathematically,
\[ \displaystyle \int_{\mathbb{R}} \textbf{u} \delta_{3D}(\xi (s) - \textbf{x}) dx = \textbf{u}_b \]
where $latex \xi(s) \in d\Omega$
Of course, the above equations are only true in the continuous world. When we switch over to the discrete world, we have to make some approximations. Firstly, we have to approximate the Dirac function because it is not always possible to have a body point lie exactly on a domain point.
Various approximations for the Dirac function are available in literature. The one most commonly used was introduced by a student of Professor Peskin in a paper in 1999. The link to the paper is available here. In the paper, the Dirac function is approximated as:
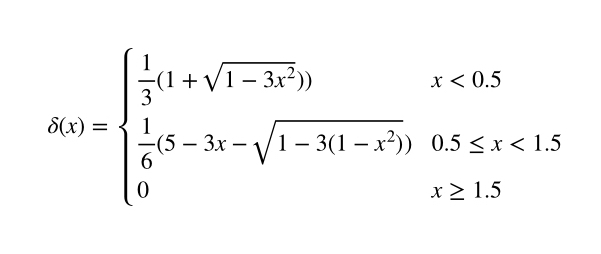
Here, $latex x$ is non-dimensionalized with the grid spacing.
Nonetheless, the Immersed Boundary Method has a fundamental branching at the very beginning of the problem. While the above method involves the forcing function directly into the continuous equations, another approach can be taken where the forcing function is brought into the equations after discretizing the Naiver-Stokes equations. Thus, we have two branches of the Immersed Boundary Method: Continuous Forcing Method, and the Discrete Forcing Method. Both methods have their merits and drawbacks.
The Continuous method forms a sound theoretical and physical understanding of the idea behind the immersed boundary method by introducing a term in the continuous equations which will enforce the no-slip and no-flow-through condition on the boundary of the object. While this method was disliked for rigid bodies due to the formation of a stiff matrix, the Immersed Boundary Projection Method (as developed by Professor Colonius and Professor Taira) has made this method highly attractive for Immersed Boundary Method implementation. The only drawback of this method is its reliance on the discretization method employed for numerical stability.
The Discrete Method applies the forcing after the discretization of the Naiver-Stokes equation. This allows for a more direct control over the numerical stability of the method. This is especially useful for moderate to high Reynolds Number applications. One major drawback of this method is its requirement of an imposing pressure (which is not required by the continuous approach). Another drawback of this method is that including boundary motion into the discrete equations can be difficult to implement.
One drawback of the Immersed Boundary Method is its inability to exactly satisfy the conservation equations due to the use of the distribution function to approximate the value of Dirac delta. Due to the distribution function, the effect of the boundary is spread into the fluid region which affects the conservation equations.
In conclusion, the Immersed Boundary Method allows us to solve for an immersed boundary (object) inside a fluid (rigid or elastic). This method is extremely useful as it allows us to solve for the immersed object without forming a body-conforming grid around it. The method, while being unable to exactly conserve the fluid properties, is an excellent approximation to a complex problem. The great advantage of this method is that we can use a traditional Cartesian grid for the flow field which allows us to quickly solve the discretized Navier-Stokes equations.
This method can be extended to conserve any fluid property once we have obtained the velocity distribution of the flow for an incompressible Newtonian fluid (like temperature, species, etc.).
One can refer to Professor Colonius and Professor Taira’s paper here, and Professor Mittal and Professor Iaccarino’s paper here for more details and a thorough overview on the subject.